什么是激活函数:
下午学完了神经网络误差的反向传播,心满意足看着满屏幕刚撸出来的Affine,Sigmoid,ReLU,Softmax……突然,心里发出一声疑问:激活函数有什么用???我慌了,我说不上来,但是隐隐约约能知道这玩意是干嘛的,本着一贯刨根问底跑个稀烂的作风,我决定彻底搞清楚!
引例
首先回到机器学习最初始的那个地方—–逻辑门(感知机表示)
1 | #与门感知机 |
1 | #或门感知机 |
1 | #与非门感知机 |
毫无技术含量,所以这里就不细讲代码。
接下来看看如何表示异或门:
1 | def XOR(x1,x2): |
显然异或门的实现借助了另外三个门!
下面从几何角度上看看异或门: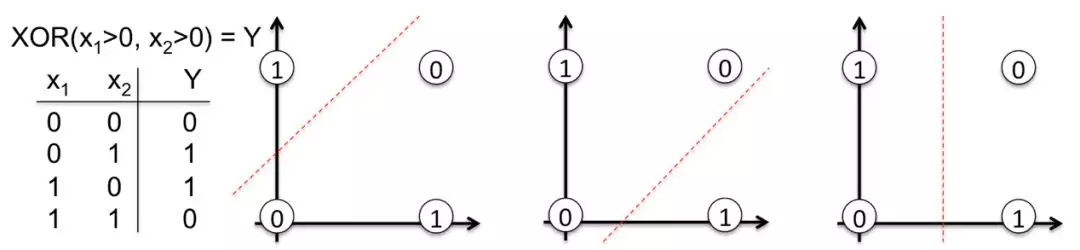
显然:异或门划分的空间是非线性的!而另外三个门划分都是线性的!
现在再回头思考,发现通过对简单门的叠加,实现了非线性划分空间的复杂门!
回到神经网络中
神经网络中,我们知道,隐藏层中主要是Affine层和各种激活函数层: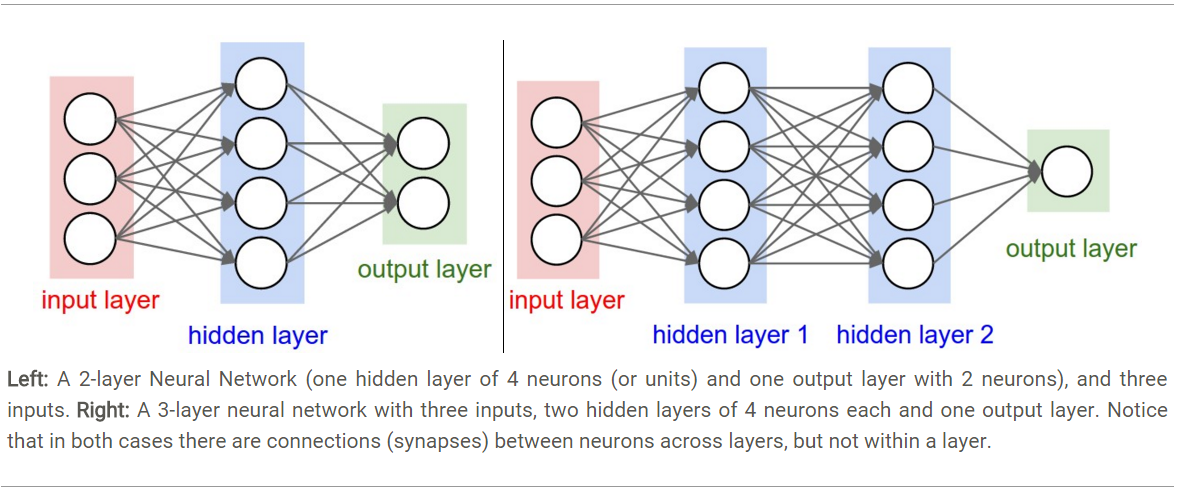
现在假设把激活函数都删掉,也就是说经过一层仿射变换后不加处理继续下一层仿射变换。
比如:x->w·x=y->w’·y=z…(矩阵点乘)
这样会有什么问题呢?很显然。
注意: x->w·x=y->w’·y=z就相当于z=cx,其中c=w·w’
这说明两层仿射变换后的表达式结构还是线性的!!同理n层之后还是线性!这简直是无用功!要记住,神经网络那么多层的目的是尽可能学习如何逼近数据,如果数据是非线性结构排布的,那叠加再多也毫无卵用!
所以现在再来看看这个问题:为什么需要激活函数?
总结一下:
如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下你每一层节点的输入都是上层输出的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,这种情况就是最原始的感知机(Perceptron)了,那么网络的逼近能力就相当有限。正因为上面的原因,我们决定引入非线性函数作为激励函数,这样深层神经网络表达能力就更加强大(不再是输入的线性组合,而是几乎可以逼近任意函数)
