今天看完🐟书后回头捋了一下，突然对ReLU激活函数产生了疑问。

引例

试想一下有X1，X2两个输入，对应三个输出的简易网络：

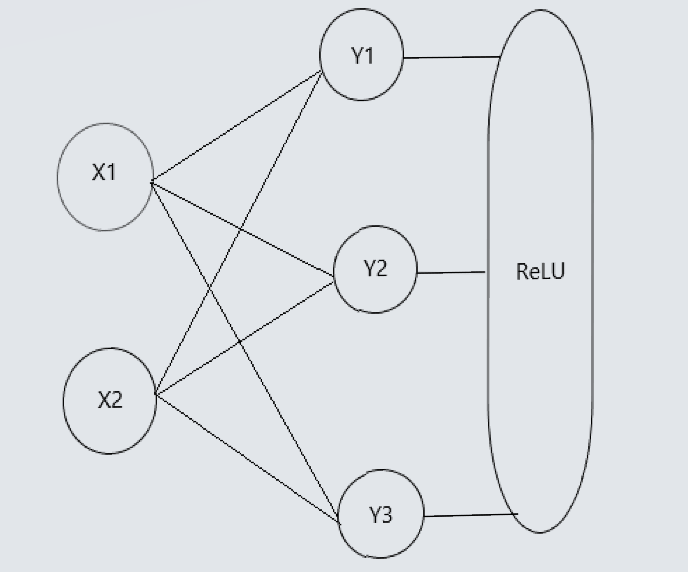
根据对应把权值W设为W11,W12,W13…W23
显然通过矩阵运算：

Y1=W11·X1+W21·X2
Y2=W12·X1+W22·X2
Y3=W13·X1+W23·X2

所得到的表达式依旧是X的线性表达式
之后通过ReLU层（这里假设都>0）
因为Y1，Y2，Y3＞0，故输出不变：

Y1=W11·X1+W21·X2
Y2=W12·X1+W22·X2
Y3=W13·X1+W23·X2

问题提出

我们知道引入激活函数的目的是为了使层神经网络表达能力就更加强大（不再是输入的线性组合，而是几乎可以逼近任意函数，详见上篇Blog），而通过小实验发现，ReLU好像并没有改变原式的线性结构，反而是原式输出。那么是否有悖机器学习的原理呢？

问题解决

首先肯定一点：上面的实验确实反映了ReLU没有改变实验对象的线性结构。

下面细说：

首先观察实验，实验的基础是Y1,Y2,Y3＞0这个条件，在这个条件下显然是等价于恒等函数的。也就是说Y被原样加工。因为原来的表达式是线性结构，所以激活之后依旧是线性结构。但是，这并不能说明ReLU对增强神经网络的表现力无用。

事实是，参与训练的数据首先不止2个（参考MNIST数据集，训练输入就6万个），其次对权值w的初始化是按标准差为0.01的高斯分布来进行的，这就肯定输入ReLU层的数据不恒正！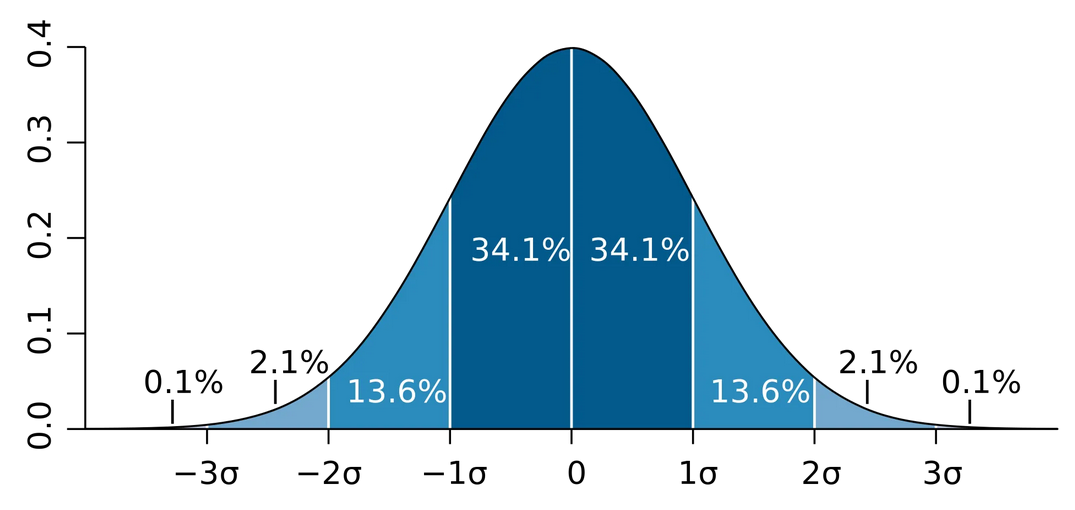

而小于0的则被赋值0，这意味着什么呢？线性结构被破坏！

用矛盾推理法来想一下这个问题（假设ReLU不改变线性结构）：

• 那么应改满足F(X)=M·X（矩阵乘法）——>ReLU ——>M·X——>G(F(X))=N·M·X——>ReLU ——>N·M·X…
• 可事实是：权值的正态性不保证每次输入都是正值，所以中间会出现等于0的情况
• 也就是F(X)=M·X（矩阵乘法）——>ReLU ——>0——>G(0）！=N·M·X——>…
• 显然线性传递被中断
• 或者说形成了一个新的线性空间，新空间与恒等线性空间互相无法表示，使整个空间呈非线性结构