废话不多说,俺先讲一下来龙去脉~
今天看鱼书P108页,遇到一个想不通的地方,我先放一波源码:
(不了解的小伙伴看上一篇博文,有源码连接)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
x = np.array([0.6, 0.9])
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
print(dW)
|
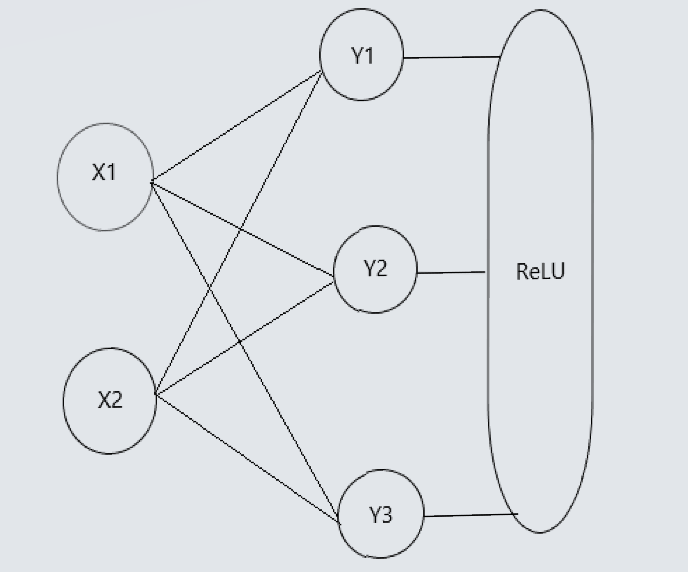
没错,这个是一个求神经网络梯度 w 的简单脚本。
如你所见,文件头也import了许多外部函数,下面贴其中一个比较重要的外部函数:
numerical_gradient函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
import numpy as np
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val
it.iternext()
return grad
|
下面讲讲这个坑
小伙子们注意看第一段代码28,29两行:
1
2
| f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)
|
函数f中lambda表达式没什么问题,注意里面的参数 w ,仔细看,你会发现……卧槽!这不没jb卵用吗…
如果你这么想,那你跟年轻的我有的一拼,too young,too simple
接着看下一行:dW = numerical_gradient(f, net.W)很显然调用了numerical_gradient函数,没毛病。但是,兄弟萌,请仔细看看numerical_gradient函数实现机制,你会发现:
第13行: fxh1 = f(x)
第16行: fxh2 = f(x)
??????????
看不出问题吗?
注意:这里的f是:
1
| f = lambda w: net.loss(x, t)
|
w是伪参数,没卵用,而x是net.W——神经网络的权重组成的数组,这尼玛驴头不对马嘴怎么就传给f了???而且f也不需要参数啊!
我是左思右想一下午,后来有了一个猜想来解释这段代码。
猜想
我猜想fxh1 = f(x) ,fxh2 = f(x)括号里的x对程序根本没卵用,于是我大胆的删掉了x,变成:
第13行: fxh1 = f()
第16行: fxh2 = f()
当然为了保持兼容,也得把lambda表达式那个伪参数删了:
f = lambda : net.loss(x, t)
然后编译运行,结果…tmd就对了,你肯定觉得这是个坑,没错,我开始也觉得是坑,坑死我了。
后来浏览了后面的代码,发现了一些用numerical_gradient函数做测试脚本,其中测试的是一些简单函数的梯度问题,涉及到变量x所以numerical_gradient函数的x要保留。。。。。。相应的,神经网络求梯度就要顺着numerical_gradient函数,没必要再写一个,于是就加了伪参数w保证兼容。
最后俺深刻的明白:实践是检验真理的唯一标准(早试试就不会浪费那么多时间了)